How To Use Notch Filters – C# Guide
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired...
Filter by Category
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired...
Bandpass filters are the counterpart of bandreject filters. Therefore, they attenuate every frequency outside the ring. In case you’re just tuning in, let me clarify what I...
We use bandreject filters to attenuate a ring of frequencies around the center of a 2 dimensional frequency map. Now what does all that mean? We’re going to focus on...
We use Laplacian filter to sharpen images. We are going to talk about the details how exactly this filter works. In essence, it’s one of the highpass filters, which...
Gaussian highpass filter processes images in frequency domain. It attenuates low frequencies without creating ringing artifacts.
Butterworth highpass filter is used to filter images in frequency domain. We can control how smooth transition beyond cut off frequency.
Ideal highpass filter is used to filter images in the frequency domain. It attenuates low frequencies and keeps high frequencies.
We’ve talked about ideal lowpass filter and Butterworth lowpass filter already. And now, we shall get to know the last type of lowpass filters, which is Gaussian lowpass...
Butterworth lowpass filter is used to modify images in the frequency domain.
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired from filtering in the frequency domain.
In case you’re just tuning in, I recommend checking out other posts about filtering in the frequency domain. But I’m also going to break the entire process down and give a sort of crash course here as well.
First of all, we need to transform image into frequency domain using Fourier transform. However, this transform takes two dimensional rectangle of image data. Therefore we will need to use it three times for one image, for each color channel separably.
If you’re already familiar with the transform, you will know that discrete Fourier transform takes a lot of time. Therefore we will use a more practical option, which is fast Fourier transform. However, it comes with a few contraints, before transforming our image we need to use zero padding to make it the right shape and size.
You can read more on a post that’s dedicated to Fourier transform alone. After that we’ve acquired frequency data from the transform we need to modify it with filters.
For filtering data in the frequency domain we need to multiply each frequency point with filter formula. After that, we take our filtered data and plug into inverse Fourier transform to turn it back into spatial domain.
Notch filters are probably the most useful of them all. They allow us to pass and attenuate frequencies on multiple locations over the frequency map. We can also use ideal, Butterworth and Gaussian filters to attenuate/pass frequencies smoothly.

Notch reject filters are similar to highpass filters, difference being the amount of circles of attenuated frequencies. Therefore, we have two different centers, which locations we need to calculate.
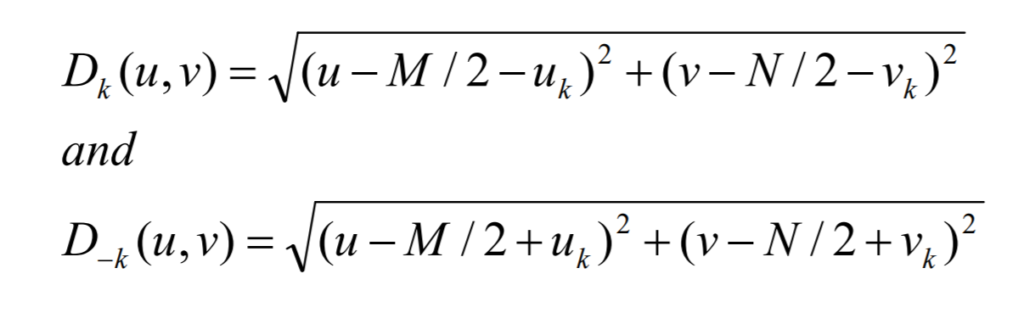
public static Complex[][][] IdealNotchRejectFilter(Complex[][][] frequencies, double d0, int[] coordinates)
{
int uoffset = coordinates[0];
int voffset = coordinates[1];
int size = FourierDemo.Size;
Complex[][][] filtered = frequencies;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < size; j++)
{
for (int k = 0; k < size; k++)
{
double d1 = Math.Sqrt(Math.Pow(j - size / 2 - uoffset, 2) + Math.Pow(k - size / 2 - voffset, 2));
double d2 = Math.Sqrt(Math.Pow(j - size / 2 + uoffset, 2) + Math.Pow(k - size / 2 + voffset, 2));
if ((d1 <= d0 || d2 <= d0) || !(d1 > d0 || d2 > d0))
{
filtered[i][j][k] *= 0f;
}
}
}
}
return filtered;
}Code above implements the ideal notch reject filter shown in the Fourier transform spectrum image above.
Every ideal filter has a simple formula, but it’s a different story for Butterworth filters. In addition Butterworth filters allow us to control the fade between attenuated and passed frequencies.

Notch filters also allow filtering with multiple pairs and following formula shows this with Butterworth notch reject filters.
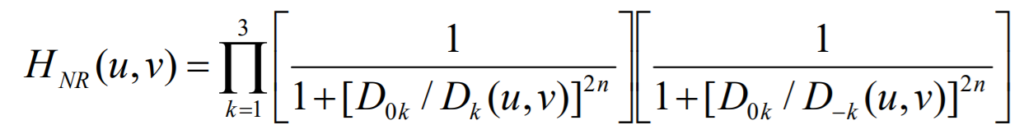
public static Complex[][][] ButterworthNotchRejectFilter(Complex[][][] frequencies, double d0, int[] coordinates, int order)
{
int uoffset = coordinates[0];
int voffset = coordinates[1];
Complex[][][] filtered = frequencies;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < Size; j++)
{
for (int k = 0; k < Size; k++)
{
double d1 = Math.Sqrt(Math.Pow(j - Size / 2 - uoffset, 2) + Math.Pow(k - Size / 2 - voffset, 2));
double d2 = Math.Sqrt(Math.Pow(j - Size / 2 + uoffset, 2) + Math.Pow(k - Size / 2 + voffset, 2));
filtered[i][j][k] *= (float)(1f / (1 + Math.Pow(d0 / d1, 2 * order))) * (float)(1f / (1 + Math.Pow(d0 / d2, 2 * order)));
}
}
}
return filtered;
}Function above demonstrates the use of one Butterworth notch reject filter pair.
We can get formulation for all notch pass filters with notch reject filter formulas. Following formula show’s how we achieve this.
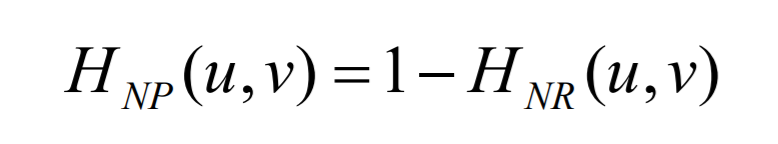
I recommend checking out project where you can also examine the use of Gaussian notch reject filter. Hopefully this tutorial has proven to be helpful and instructive.