How To Use Bandreject Filters – C# Guide
We use bandreject filters to attenuate a ring of frequencies around the center of a 2 dimensional frequency map. Now what does all that mean? We’re going to focus on...
Filter by Category
We use bandreject filters to attenuate a ring of frequencies around the center of a 2 dimensional frequency map.
Now what does all that mean?
We’re going to focus on filtering images in the frequency domain. Firstly, we need to transform image data into frequency domain with Fourier transform. In case you’re not familiar with the transform, it takes a 2 dimensional map of image data and transforms it into a 2 dimensional map of frequency data the same size as the image. So we need to use it 3 times for each image to process all 3 color channel.
Secondly, any kind of filtering in the frequency domain works by multiplying filter formula with all of the values in the frequency map. These formulas contain parameters that set the location of the frequencies we want to attenuate.
There are three bandreject filters we can use, which differ in the transition between passed and attenuated frequencies. These three filters are Ideal, Butterworth and Gaussian bandreject filters.
Bandreject filters work similarly to lowpass filters. The Difference being that bandreject filters attenuate frequencies before cut off frequency as well.
This filter’s formula isn’t all that complicated. The transition between attenuated and passed frequencies is instant.

Let’s also take a look at the code that makes this work.
public static Complex[][][] IdealBandrejectFilter(Complex[][][] frequencies, double d0, double W)
{
Complex[][][] filtered = frequencies;
for (int i = 0; i < 3; i++)
{
for (int u = 0; u < Size; u++)
{
for (int v = 0; v < Size; v++)
{
double d = Math.Sqrt((Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2)));
if (d >= (d0 - W/2) && d <= (d0 + W/2))
{
filtered[i][u][v] *= 0f;
}
}
}
}
return filtered; }To put this into words, the frequencies that are located in the ring are removed. We can control the width of the ring with parameter W and radius by parameter d0.
With this filter we’re able to control a little bit more. In addition, we can use an additional parameter which is the order of the filter. If we set order to be low, like 2 or 3, it will act more like a Gaussian filter. But if we set it high, like 20, it will act like an ideal filter. It controls how smooth the transition between attenuated and passed frequencies is.

Because of a larger cut off frequency and smooth transition between frequencies the effect looks faintly visible.
Butterworth bandreject filter also has its own formula.
As we mentioned before at the ideal bandreject filter, W and D0 stand for width of the ring and radius of cut off frequency, respectively. D, on the other hand, stands for the distance from center for each frequency. And we calculate it with the following formula.
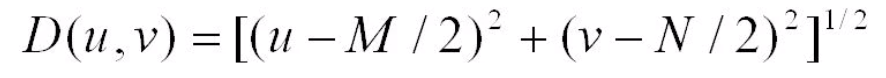
Here M and N represent the dimensions of the frequency map, width and height.
Let’s take a look at the C# function that applies it.
public static Complex[][][] ButterworthBandrejectFilter(Complex[][][] frequencies, double d0, int n, double W)
{
Complex[][][] filtered = frequencies;
for (int i = 0; i < 3; i++)
{
for (int u = 0; u < Size; u++)
{
for (int v = 0; v < Size; v++)
{
double d = Math.Sqrt((Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2)));
filtered[i][u][v] *= (float)(1f / (1 + Math.Pow(d * W / (dd - d0d0), 2 * n)));
}
}
}
return filtered;
}Gaussian bandreject filter lays on the other line of the spectrum where these three differ between each other. In other words the smoothness of the transition between attenuated and passed frequencies.
This filter has the smoothest transition and it can’t be controlled apart by setting the cut off frequency lower or higher. Therefore in that regard it’s a complete opposite from ideal bandreject filter we described earlier.
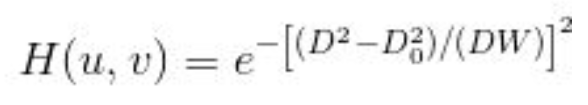
The parameters in the formula above, each stand for the same thing as in the Butterworth formula we described above.
Let’s take a look at the code that applies it as well.
public static Complex[][][] GaussianBandrejectFilter(Complex[][][] frequencies, double d0, double W)
{
Complex[][][] filtered = frequencies;
for (int i = 0; i < 3; i++)
{
for (int u = 0; u < Size; u++)
{
for (int v = 0; v < Size; v++)
{
double d = Math.Sqrt((Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2)));
filtered[i][u][v] *= (float)(1 - Math.Pow(Math.E, -(Math.Pow((Math.Pow(d, 2) - Math.Pow(d0, 2)) / d * W, 2))));
}
}
}
return filtered;
}Band reject filters are a stepping stone to band pass filters and notch filters. However, we will take a look at those in other posts. I hope this guide was helpful and instructive and I hope you’ll tune in on the next one.
You can download the project and try out the demonstration yourself.