How To Make SLIC Superpixel Algorithm With C#
SLIC superpixel segmentation is a modern operation for reducing irrelevant detail for shortening computational time in further processing.
Filter by Category
Simple linear iterative clustering or SLIC is a superpixel segmentation method for reducing irrelevant image data. Furthermore, the idea behind it is to replace standard pixel grid with a grid of regions. This way we create an image with less primitive units while preserving a descent amount of detail.
Each region, or superpixel, holds perceptually more meaningful image information than individual pixels. Therefore, since we reduce irrelevant detail, their purpose is to shorten computational time for further processing.
However, like any other image processing operation, this one also depends on the problem we’re trying to solve.
For example, it’s not acceptable for images, where we need to detect detail on pixel-level resolution, like the ones we use in medical examinations. But, it works well for those where small loss of detail doesn’t affect final results.
The way SLIC segmentation preserves detail is by adhering boundaries of superpixels to shapes of objects and background. Therefore it preserves details of shapes, while reducing color detail of the image overall.
In case we wanted to preserve a lot of detail, we could just increase the amount of superpixels. Since each of them will represent a region of individual pixels, our resulting image would still save up on space and computational time for further processing.
SLIC operation is a modification of k-means clustering, which we already covered in another article. In case you’re not familiar with it, I would suggest you check it out. This tutorial will be a walk in the park if you understand how that works.
First of all, we’re going to represent each pixel with a feature vector, which will hold color and spatial information. Therefore, each vector will hold 5 values, first three for RGB values and last two for horizontal and vertical position.
To begin with the process, we need to initialize it by choosing starting pixels for superpixel centers. In order to do that, we need to sample them so we end up with a grid of these points.
Furthermore, we’re going to use the following formula to compute this interval. Or in other words distance between each center in x and y position.
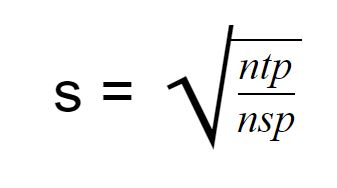
For some context ntp represents the number of all pixels in the image and nsp
While we’re sampling these starting superpixel centers, we need to check for the lowest gradient point in 3×3 neighborhood. Reason for that is so we don’t set our centers on noisy pixels. Therefore, I used Sobel edge detection operation to find those.
Next step is assigning pixels to their closest centers by computing pixel distance in a 2sx2s neighborhood around each center.
We’re going to use the following formula to compute distances between superpixel centers and pixels around them.
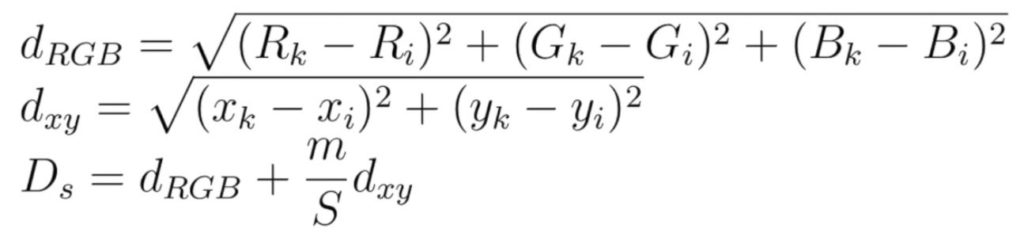
After we assigned pixels to each center, we need to update the position and mean color values for each center.

Next step is to test whether we need to repeat the process from assigning pixels again or not. Therefore, we need to compute an error value. We can do that by summing Euclidean distances of all superpixel center values from current and previous steps.
In order to stop looping this whole process, we need to set a threshold. So when the error value will be lower or equal to it, algorithm will close the loop. I my case here I set it to error from previous step.
And for our final step we’re going to set each pixel their respective superpixel color.

public static Bitmap Superpixels(this Bitmap image, int nsp)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int ntp = buffer.Length / 3;
int s = (int)Math.Floor(Math.Sqrt((double)ntp / nsp));
int[][] means = new int[nsp][];
byte[] result = new byte[bytes];
int sp = 0;
//compute initial superpixel cluster centers
for (int x = s / 2; x < w; x+=s)
{
for (int y = s / 2; y < h; y+=s)
{
int position = x * 3 + y * image_data.Stride;
//compute lowest gradient
int lowest_grad = 99999;
for (int i = -1; i <= 1; i++)
{
for (int j = -1; j <= 1; j++)
{
int n_pos = position + i * 3 + j * image_data.Stride;
int grad = 0;
for (int k = -1; k <= 1; k++)
{
for (int l = -1; l <= 1; l++)
{
int g_pos = n_pos + k * 3 + l * image_data.Stride;
grad += buffer[g_pos] * (Filters.SobelHorizontal[k + 1, l + 1] + Filters.SobelVertical[k + 1, l + 1]);
}
}
if (lowest_grad > grad)
{
lowest_grad = grad;
means[sp] = new int[] { buffer[n_pos], x + i, y + j };
}
}
}
for (int c = 0; c < 3; c++)
{
result[means[sp][1] * 3 + means[sp][2] * image_data.Stride + c] = 255;
}
if (sp < nsp - 1)
{
sp++;
}
}
}
int[] labels = new int[bytes];
double[] distances = new double[bytes];
for (int i = 0; i < bytes; i+=3)
{
labels[i] = -1;
distances[i] = buffer.Length;
}
double error = new double();
double cc = 20;
while (true)
{
int[][] new_means = new int[nsp][];
//assign samples to clusters
for (int i = 0; i < nsp; i++)
{
int m_pos = means[i][1] * 3 + means[i][2] * image_data.Stride;
int xe = 2 * s + means[i][1];
int xs = means[i][1] - 2 * s;
int ye = 2 * s + means[i][2];
int ys = means[i][2] - 2 * s;
for (int x = (xs < 0 ? 0 : xs); x < ((xe < w) ? xe : w); x++)
{
for (int y = (ys < 0 ? 0 : ys); y < (ye < h ? ye : h); y++)
{
int position = x * 3 + y * image_data.Stride;
double ds = Math.Sqrt(Math.Pow(x - means[i][1], 2) + Math.Pow(y - means[i][2], 2));
double dc = Math.Sqrt(Math.Pow(buffer[position] - means[i][0], 2)
+ Math.Pow(buffer[position + 1] - means[i][0], 2)
+ Math.Pow(buffer[position + 2] - means[i][0], 2));
double distance = dc + (cc / s) * ds;
if (distance < distances[position])
{
distances[position] = distance;
labels[position] = i;
}
}
}
}
//compute new means
for (int i = 0; i < nsp; i++)
{
new_means[i] = new int[3];
int samples = 0;
for (int x = 0; x < w; x++)
{
for (int y = 0; y < h; y++)
{
int position = x * 3 + y * image_data.Stride;
if (labels[position] == i)
{
new_means[i][0] += buffer[position];
new_means[i][1] += x;
new_means[i][2] += y;
samples++;
}
}
}
for (int j = 0; j < 3; j++)
{
new_means[i][j] /= samples;
}
}
//compute error
double new_error = 0;
for (int i = 0; i < nsp; i++)
{
new_error += (int)Math.Sqrt(Math.Pow(means[i][0] - new_means[i][0], 2)
+ Math.Pow(means[i][1] - new_means[i][1], 2)
+ Math.Pow(means[i][2] - new_means[i][2], 2));
means[i] = new_means[i];
}
if (error < new_error)
{
break;
}
else
{
error = new_error;
}
}
for (int i = 0; i < nsp; i++)
{
for (int j = 0; j < bytes; j+=3)
{
if (labels[j] == i)
{
for (int c = 0; c < 3; c++)
{
result[j + c] = (byte)means[i][0];
}
}
}
}
Bitmap res_img = new Bitmap(w, h);
BitmapData res_data = res_img.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
Marshal.Copy(result, 0, res_data.Scan0, bytes);
res_img.UnlockBits(res_data);
return res_img;
}I hope this tutorial helped you understand how superpixel segmentation works.
You can also download the demo project and try it out yourself.
Comments
Hello,
I’m having trouble getting your code to work, but that’s okay – I’m going to stick with it.
I wanted to point out that your “compute new means” code could be faster. If you set up your new means arrays as well as an array of counters, you’ll increase the storage necessary, but you’ll also be able to iterate over the labels instead of iterating over the superpixels, then iterating over all of the pixels and then finding out if those pixels had been found to be inside that superpixel.
After you do this, you can do the necessary division inside one loop over the superpixels.
This changes it from being a triply-nested for-loop to being 3 single for-loops.
I haven’t gotten to test this yet, but I’ll let you know when I get it working. I had to make significant modifications for my purposes, but the theory and structure remains unchanged.