How To Make Alpha Trimmed Mean Filter For Images
Alpha trimmed mean filter is a combination of mean filters and order-statistic filters. This guide shows how to use them with C#.
Filter by Category
Alpha trimmed mean filter is a combination of mean filters and order-statistic filters. This guide shows how to use them with C#.
Midpoint filter is a order-statistic filter and we use it to process image data in spatial domain. This guide shows how to make it with C#.
Max and min filter is one of the order-statistic filter we can use to process image data in spatial domain. This tutorial shows it with C#.
Median filter is one of the order-statistic filters for processing image data in spatial domain. This guide shows how to apply it with C#.
We use alpha trimmed mean filter to process image data in spatial domain. Furthermore, it’s one of the most useful order-statistic filters, because we can use it to reduce combined noises from images.
Order-statistic filters are spatial filters and this one is no exception. Therefore, to process image in spatial domain, we will need to move the filter across it. In other words, spatial filters act as a small window that encompasses pixels that fit inside.
It processes the encompassed image data inside it and outputs one intensity value per filter position. So we need to move it one pixel at a time to filter the entire image. Because of this process, our output image will have slightly smaller dimensions.
We can counteract this by zero padding our image and expand its dimensions before filtering to compensate for the loss.
This filter is a special case, because it can reduce either to arithmetic mean filter or to median filter. It depends on d variable we’ll see in the following formula. It basically trims lowest and highest intensity values from the set.
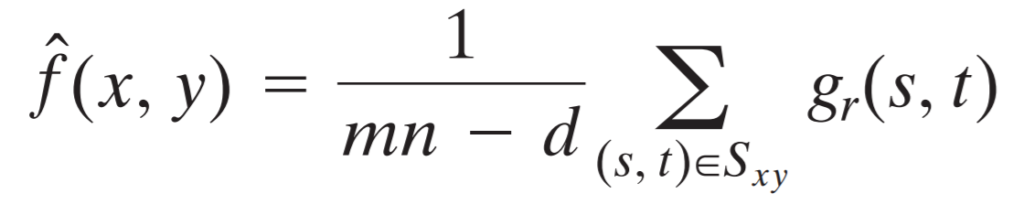
Okay, let’s break it down. The gr(s, t) function represents all the remaining intensity values in the set after, we’ve already removed extreme values.
The mn is the product of filter dimensions, which also means, it’s the total of all the values inside the filter. Therefore, if we set the d variable to 0, our filter becomes the same as arithmetic mean filter. On the other hand, if we set it to mn – 1, the filter becomes the median filter.
I wrote a function, which takes all values encompassed by the filter and stores them in array. After that, it removes the same amount of lowest and highest intensity values and computes output intensity value. To set the d variable, we set it as function parameter, but we need to set it’s halved value.
public static Bitmap Filter(this Bitmap image, int half_d)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int r = 1;
int wres = w - 2 * r;
int hres = h - 2 * r;
Bitmap result_image = new Bitmap(wres, hres);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, wres, hres),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
int res_bytes = result_data.Stride * result_data.Height;
byte[] result = new byte[res_bytes];
for (int x = r; x < w - r; x++)
{
for (int y = r; y < h - r; y++)
{
int pixel_location = x * 3 + y * image_data.Stride;
int res_pixel_loc = (x - r) * 3 + (y - r) * result_data.Stride;
double[] median = new double[3];
int[][] neighborhood = new int[3][];
for (int c = 0; c < 3; c++)
{
neighborhood[c] = new int[(int)Math.Pow(2 * r + 1, 2)];
int added = 0;
for (int kx = -r; kx <= r; kx++)
{
for (int ky = -r; ky <= r; ky++)
{
int kernel_pixel = pixel_location + kx * 3 + ky * image_data.Stride;
neighborhood[c][added] = buffer[kernel_pixel + c];
added++;
}
}
for (int i = 0; i < half_d; i++)
{
int min_idx = Array.IndexOf(neighborhood[c], neighborhood[c].Min());
int max_idx = Array.IndexOf(neighborhood[c], neighborhood[c].Max());
neighborhood[c] = neighborhood[c].Where((val, idx) => idx != min_idx).ToArray();
neighborhood[c] = neighborhood[c].Where((val, idx) => idx != max_idx).ToArray();
}
}
for (int c = 0; c < 3; c++)
{
result[res_pixel_loc + c] = (byte)((1 / (Math.Pow(2 * r + 1, 2) - 2 * half_d)) * neighborhood[c].Sum());
}
}
}
Marshal.Copy(result, 0, result_data.Scan0, res_bytes);
result_image.UnlockBits(result_data);
return result_image;
}
Alpha trimmed mean filter is kind of an universal order-statistic/mean filter, since we can change it into others. But not only that, it can also become something in between and that’s why it even trumps median filter.
I hope this guide was helpful. You can also download the entire project and test it out on your own images.