How To Use Arithmetic Mean Filter On Images – C# Guide
Arithmetic mean filter is one of the simplest mean filters we could use to reduce noise from an image. Learn more about spatial filtering.
Filter by Category
Arithmetic mean filter is one of the simplest mean filters we could use to reduce noise from an image. Learn more about spatial filtering.
Salt and pepper noise or impulse noise is one of the noise models we can use to simulate image data corruption in real life.
Uniform noise is one of the noise models we can use to simulate real life data corruption. This guide shows how to make in on images.
Exponential noise is one of the noise models we can use to simulate corruption of data. This guide show how to use it on images.
Gamma noise is one of the noise models we use to simulate practical data corruption. This guide shows how to apply it on images.
Rayleigh noise is one of the noise models with which we can simulate data corruption. Guide to making noise from PDF and image histogram.
Gaussian noise on images is generated with Gaussian probability distribution function. It simulates noise that appears in practice.
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired...
Bandpass filters are the counterpart of bandreject filters. Therefore, they attenuate every frequency outside the ring. In case you’re just tuning in, let me clarify what I...
We use bandreject filters to attenuate a ring of frequencies around the center of a 2 dimensional frequency map. Now what does all that mean? We’re going to focus on...
We use arithmetic mean filter for processing images in the spatial domain. Therefore, we will use a kernel and convolution to get our output values.
Mean filters are generally most useful for filtering images, that only have noise degradation. In other words, we don’t need to worry about any other image alteration than that.
We mentioned we will be needing a kernel to filter our image data. In case you’re wondering what is it, it’s basically a small matrix of coefficients. Furthermore, we place this matrix on our image and compute new pixel values with convolution.
And to clearify what convolution is, it’s essentially moving kernel accross the entire image to change every pixel by multiplying it and it’s surrounding pixels with our kernel.
This type of mean filter is one of the simplest we could use. However, the noise reduction comes with a cost of blurring the image.
Arithmetic mean filter calculates the average value in a set of pixel values. In other words, we sum up all pixel values within the set and divide them by the size of that set. Convolution works by multiplying each coefficient in the kernel that coincides with the pixel value and summing it all up to form output value in the center of it.
This way our arithmetic mean filter kernel would have the same coefficient in all of it’s fields, which is 1/mn. The m and n represent dimension of our kernel. To simplify all this, the following formula shows how each value in the output image is computed.
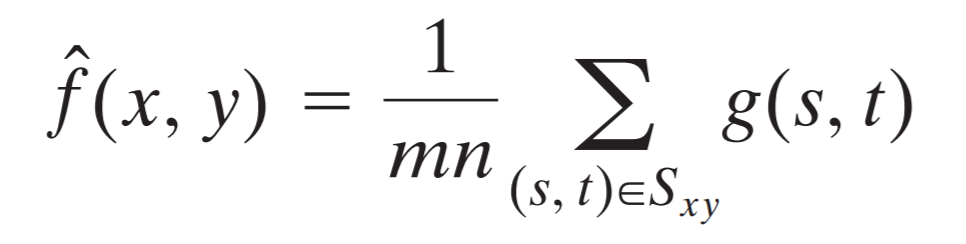
The g(s, t) function represents pixel value of our corrupted image on s and t coordinates inside the kernel window.
Be aware that this kind of filtering will change the size of the output image. Therefore, in order to prevent that from happening, you should use zero padding to compensate for the size reduction.
I’ve written several functions in this project, which affect the image in one way or the other. However, the following one does the heavy lifting and applies the arithmetic mean filter. But if you’re interested, I’ve also used image zero padding, and scaling for display purposes.
public static Bitmap ArithmeticMean(this Bitmap image)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int r = 1;
int wres = w - 2 * r;
int hres = h - 2 * r;
Bitmap result_image = new Bitmap(wres, hres);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, wres, hres),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
int res_bytes = result_data.Stride * result_data.Height;
byte[] result = new byte[res_bytes];
for (int x = r; x < w - r; x++)
{
for (int y = r; y < h - r; y++)
{
int pixel_location = x * 3 + y * image_data.Stride;
int res_pixel_loc = (x - r) * 3 + (y - r) * result_data.Stride;
double[] mean = new double[3];
for (int kx = -r; kx <= r; kx++)
{
for (int ky = -r; ky <= r; ky++)
{
int kernel_pixel = pixel_location + kx * 3 + ky * image_data.Stride;
for (int c = 0; c < 3; c++)
{
mean[c] += buffer[kernel_pixel + c] / Math.Pow(2 * r + 1, 2);
}
}
}
for (int c = 0; c < 3; c++)
{
result[res_pixel_loc + c] = (byte)mean[c];
}
}
}
Marshal.Copy(result, 0, result_data.Scan0, res_bytes);
result_image.UnlockBits(result_data);
return result_image;
}When we’re filtering image data in the spatial domain, we need to get familiar with the standard process of convolution. Once we get the hang of that, understanding how spatial filters work will be a walk in the park.
I hope this guide was helpful and I hope you stick around for more. You can also download the project and try it out yourself.