We’ve talked about ideal lowpass filter and Butterworth lowpass filter already. And now, we shall get to know the last type of lowpass filters, which is Gaussian lowpass filter.

I imagine you’re already familiar with the workings of Fourier transform pair and filtering in the frequency domain. And in case you just heard about it now and want to know more, please check out other posts on this topic. I’ll try my best to keep things short and concise.

Gaussian lowpass filter

Lowpass filters in general modify frequency map by removing high frequencies and passing through only low frequencies. High frequencies carry information of sharp transition between colors in spatial domain like edges or noise.

By removing high frequencies we essentially blur the image. And I already made a post how to create Gaussian blur on images by convoluting Gaussian filter in the spatial domain.

Gaussian lowpass filter differs from other lowpass filters in smooth transition beyond cut off frequency. This cut off frequency acts as a circular border around the center of the frequency map beyond which higher frequencies begin to fade to 0.

We can control how blurred the output image will be by setting the radius of the circle. The smaller the circle of passed frequencies in the middle will be, blurier the image will get.

To calculate filter values we use the following formula:

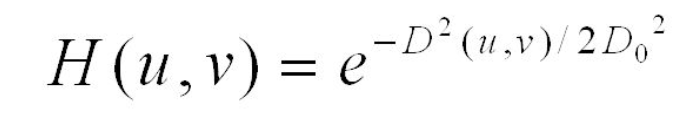
Where D(u,v) is calculated as:

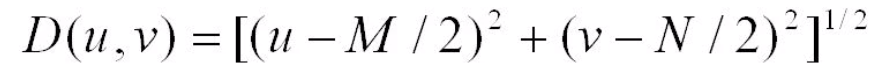
M and N are the same size in the function as follows. That’s because Fast Fourier transform accepts only square images with 2ⁿ being the size of each dimension.

public static Complex[][][] Gaussian_Lowpass_Filter(Complex[][][] frequencies, double distance)
         {
             int channels = 3;
             Complex[][][] filtered = frequencies;
             for (int c = 0; c < channels; c++)
             {
                 for (int u = 0; u < Size; u++)
                 {
                     for (int v = 0; v < Size; v++)
                     {
                         double d = Math.Sqrt(Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2));
                         filtered[c][u][v] *= (float)(Math.Pow(Math.E, -Math.Pow(d, 2) / (2 * Math.Pow(distance, 2))));
                     }
                 }
             }
         return filtered;
     }

Unwanted artifacts

When we use ideal and Butterworth lowpass filters we can get some unwanted artifacts (color blobs) on our image. We call it ringing and it appears because the fading border around the circle of passed frequencies is too thin.

With Ideal lowpass filter there is no fading beyond cut off frequency much like cutting cookie doe shapes.

Butterworth lowpass filter is more controlable because we can set its order to set the width of the fading border around the circle. The higher the order is, thinner the border gets. Usually if we use orders of 3 and above, we can experience ringing.

Gaussian lowpass filter doesn’t have such problem because the fading border is always thick enough. If we’re processing images where artifacts are super unwanted, like images for medical purposes, this is the filter to go with. But if you want to have control over the filter and its thickness of the fading border, Butterworth lowpass filter would be the right choise.

Conclusion

Hopefully this guide was undestandable and helpful. You can also download the entire project. Play with the settings yourself and see how it works line by line.

Have a good one and hope to see you in the next one.