Gaussian highpass filter is one of the highpass filters that has a lowpass counterpart. Highpass filters pass through only high frequencies and attenuates low ones.

Before we begin with filtering in the frequency domain, we should mention how to turn image into frequencies first. To transform image from spatial domain to frequency domain we need to use Fourier transform and in case you’re not familiar how the transform works, I recommend reading my post about it.

Gaussian highpass filter

Formula for Gaussian highpass filter is very similar to formula fo Gaussian lowpass filter. Of course, no surprise there, the difference between the two is that we need to subtract the Gaussian lowpass filter value from 1 and we get the value for its highpass counter part.

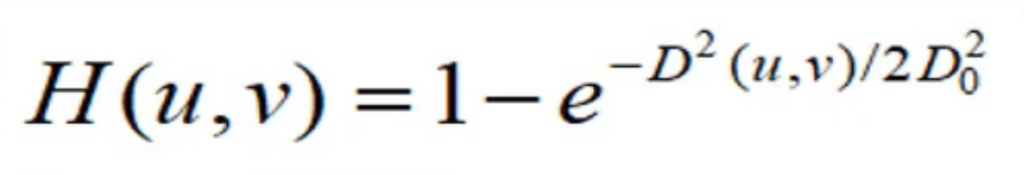
Let’s get through each part of the formula, so we can better understand what each part represents. First of all, H is a function of u and v, which represent the coordinates of the filter value.

Just to be clear, the filter is the same size as the frequency map, and consequently the image, we’re processing.

D₀ represents variable for cut off frequency, which is essentially the radius of the black hole our filter creates in the middle of our frequency map.

And finaly, D(u, v) value represents the distance of each frequency from the center of our frequency map at any given position. And it’s calculated by the following formula.

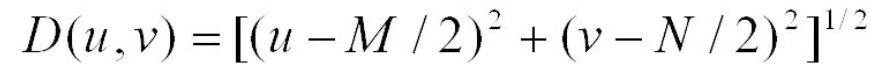
The M and N are width and height of our frequency map or image. These two are the same in our case since the fast Fourier transform algorithm takes only square images.

C# function

Following function takes a 3 dimensional jagged array of frequency values, which are in a form of complex numbers, which holds values from 3 Fourier transforms, one for each color channel. It also calculates all three frequency maps with the same cut off frequency.

public static Complex[][][] Gaussian_Highpass_Filter(Complex[][][] frequencies, double distance)
         {
             int channels = 3;
             Complex[][][] filtered = frequencies;
             for (int c = 0; c < channels; c++)
             {
                 for (int u = 0; u < Size; u++)
                 {
                     for (int v = 0; v < Size; v++)
                     {
                         double d = Math.Sqrt(Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2));
                         filtered[c][u][v] *= 1 - (float)(Math.Pow(Math.E, -Math.Pow(d, 2) / (2 * Math.Pow(distance, 2))));
                     }
                 }
             }
         return filtered;
     }

This filter is known to give a very smooth transition between the high and low frequency on the border where we set our cut off frequency.

Conclusion

You can download the entire project for free and play with the values yourself. I hope you found this tutorial helpful. Have a good one.