Exponential noise is one of the noise models we can use to simulate data corruption. In our case here, we’ll use it on images. Therefore, we will use its probability distribution function to create an image histogram and from it, noise we will add to our original image.

We encounter noise in images when we’re acquiring it. The most common reasons for it are low grade equipment and environment conditions. I other words, if we use an old camera, photos we take can end up corrupted because of lightning, temperature changes and anything that physically impacts sensors.

Exponential noise

Exponential noise is a special case of gamma or Erlang noise where b parameters equals to 1. If we take a look at the formula for gamma noise probability distribution function and input parameter b.

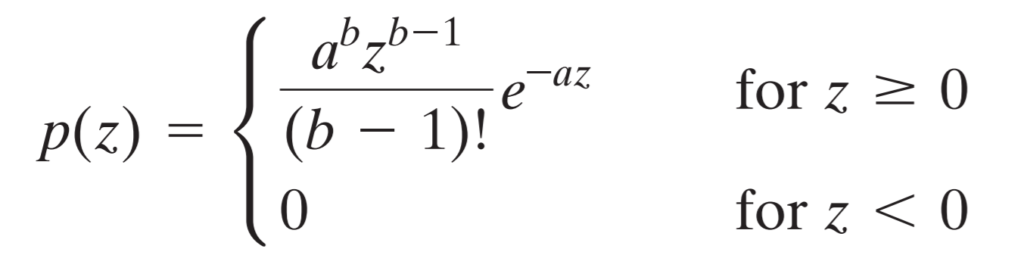
We can see that basically by eliminating the effect of parameter b, the formula for exponential noise probability distribution becomes much simpler. However, it makes the shape of the distribution curve less controlable, since we have only one parameter left for that.

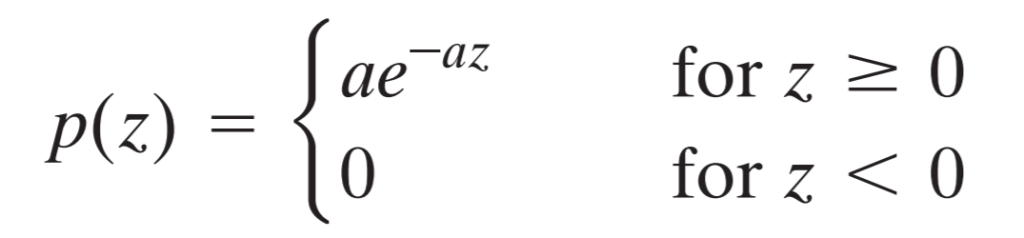
Let’s clear up what the other parameters in the formula represent. Firstly, z variable represents intensity value. Secondly, a parameter is the factor, with which we can control the shape of the exponential function curve. And lastly, e is the Eulers constant, which is 2.71828.

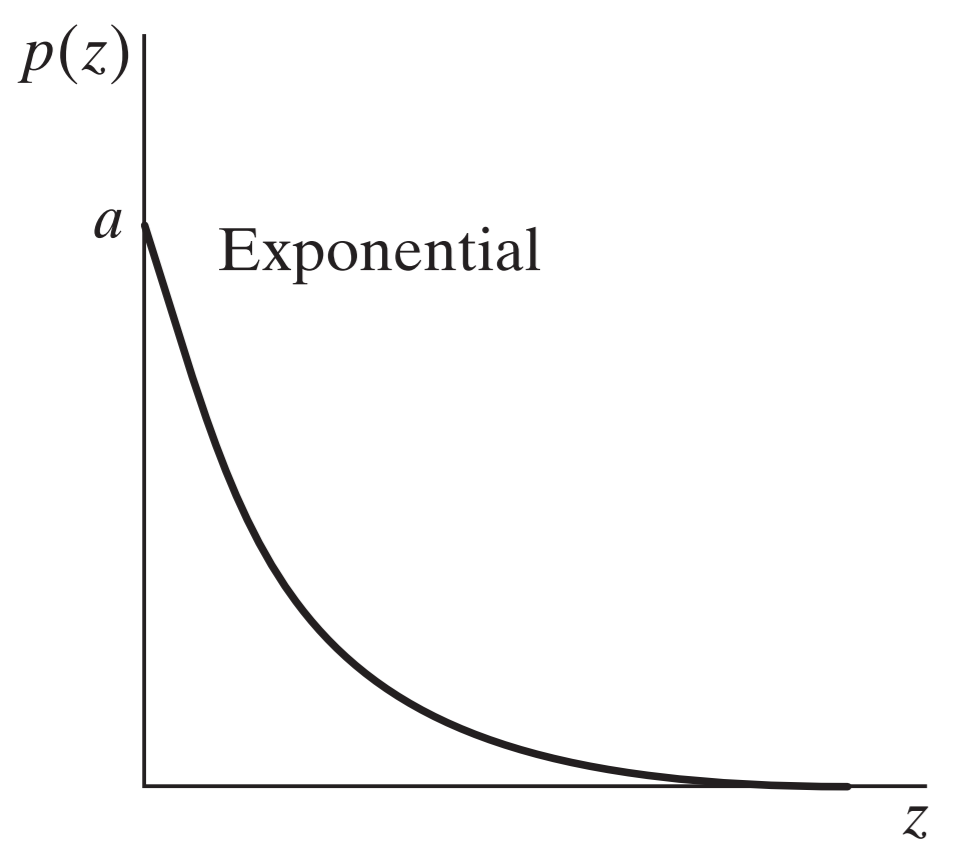
As we mentioned earlier, we will create an image histogram from the probability distribution function. Once we distributed intensity values among the pixels of the noise image we will add them to our original image te make the image noisy.

C# function

I’ll break it down what this function actually does to image data. First step is to calculate the probability distribution across all intensities. Secondly, it takes that data and divides each probability with the sum of all computed probabilities.

Furthermore, we take those normalized probabilites and multiply them by the number of pixel values original image has. After that, we take all those distributed values, put them in an array and scramble it.

public static Bitmap ExponentialNoise(this Bitmap image)
     {
         int w = image.Width;
         int h = image.Height;

         BitmapData image_data = image.LockBits(
             new Rectangle(0, 0, w, h),
             ImageLockMode.ReadOnly,
             PixelFormat.Format24bppRgb);
         int bytes = image_data.Stride * image_data.Height;
         byte[] buffer = new byte[bytes];
         byte[] result = new byte[bytes];
         Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
         image.UnlockBits(image_data);

         byte[] noise = new byte[bytes];
         double[] erlang = new double[256];
         double a = 5;
         Random rnd = new Random();
         double sum = 0;

         for (int i = 0; i < 256; i++)
         {
             double step = (double)i * 0.01;
             if (step >= 0)
             {
                 erlang[i] = (double)(a * Math.Exp(-a * step));
             }
             else
             {
                 erlang[i] = 0;
             }
             sum += erlang[i];
         }

         for (int i = 0; i < 256; i++)
         {
             erlang[i] /= sum;
             erlang[i] *= bytes;
             erlang[i] = (int)Math.Floor(erlang[i]);
         }

         int count = 0;
         for (int i = 0; i < 256; i++)
         {
             for (int j = 0; j < (int)erlang[i]; j++)
             {
                 noise[j + count] = (byte)i;
             }
             count += (int)erlang[i];
         }

         for (int i = 0; i < bytes - count; i++)
         {
             noise[count + i] = 0;
         }

         noise = noise.OrderBy(x => rnd.Next()).ToArray();

         for (int i = 0; i < bytes; i++)
         {
             result[i] = (byte)(buffer[i] + noise[i]);
         }

         Bitmap result_image = new Bitmap(w, h);
         BitmapData result_data = result_image.LockBits(
             new Rectangle(0, 0, w, h),
             ImageLockMode.WriteOnly,
             PixelFormat.Format24bppRgb);
         Marshal.Copy(result, 0, result_data.Scan0, bytes);
         result_image.UnlockBits(result_data);

         return result_image;
     }

Conclusion

This guide shows how to make a noisy image. Furthermore, making noise artificially give us opportunity to study image restoration and reconstruction techniques.

You can download the entire project and play with the values yourself.