How To Make Gamma Noise On Images – C# Guide
Gamma noise is one of the noise models we use to simulate practical data corruption. This guide shows how to apply it on images.
Filter by Category
Gamma noise is one of the noise models we use to simulate practical data corruption. This guide shows how to apply it on images.
Rayleigh noise is one of the noise models with which we can simulate data corruption. Guide to making noise from PDF and image histogram.
Gaussian noise on images is generated with Gaussian probability distribution function. It simulates noise that appears in practice.
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired...
Bandpass filters are the counterpart of bandreject filters. Therefore, they attenuate every frequency outside the ring. In case you’re just tuning in, let me clarify what I...
We use bandreject filters to attenuate a ring of frequencies around the center of a 2 dimensional frequency map. Now what does all that mean? We’re going to focus on...
We use Laplacian filter to sharpen images. We are going to talk about the details how exactly this filter works. In essence, it’s one of the highpass filters, which...
Gaussian highpass filter processes images in frequency domain. It attenuates low frequencies without creating ringing artifacts.
Butterworth highpass filter is used to filter images in frequency domain. We can control how smooth transition beyond cut off frequency.
Ideal highpass filter is used to filter images in the frequency domain. It attenuates low frequencies and keeps high frequencies.
Gamma noise is one of the noise models we can simulate on data. In our particular case, we are going to add noise to an image. Therefore, we will need to use a probability distribution function that makes that noise data.
Most commonly, the reasons for noise in images are low quality equipment and impact of environment conditions. However corruption doesn’t only happen when we’re acquiring the image, it also happens while transmitting it.
Gamma noise or Erlang noise is very similiar to Rayleigh noise regarding the shape of distribution curve. In essence, it begins with a steep slope and ends smoothly, much like Gaussian does. We can see what we just described in the following graph.
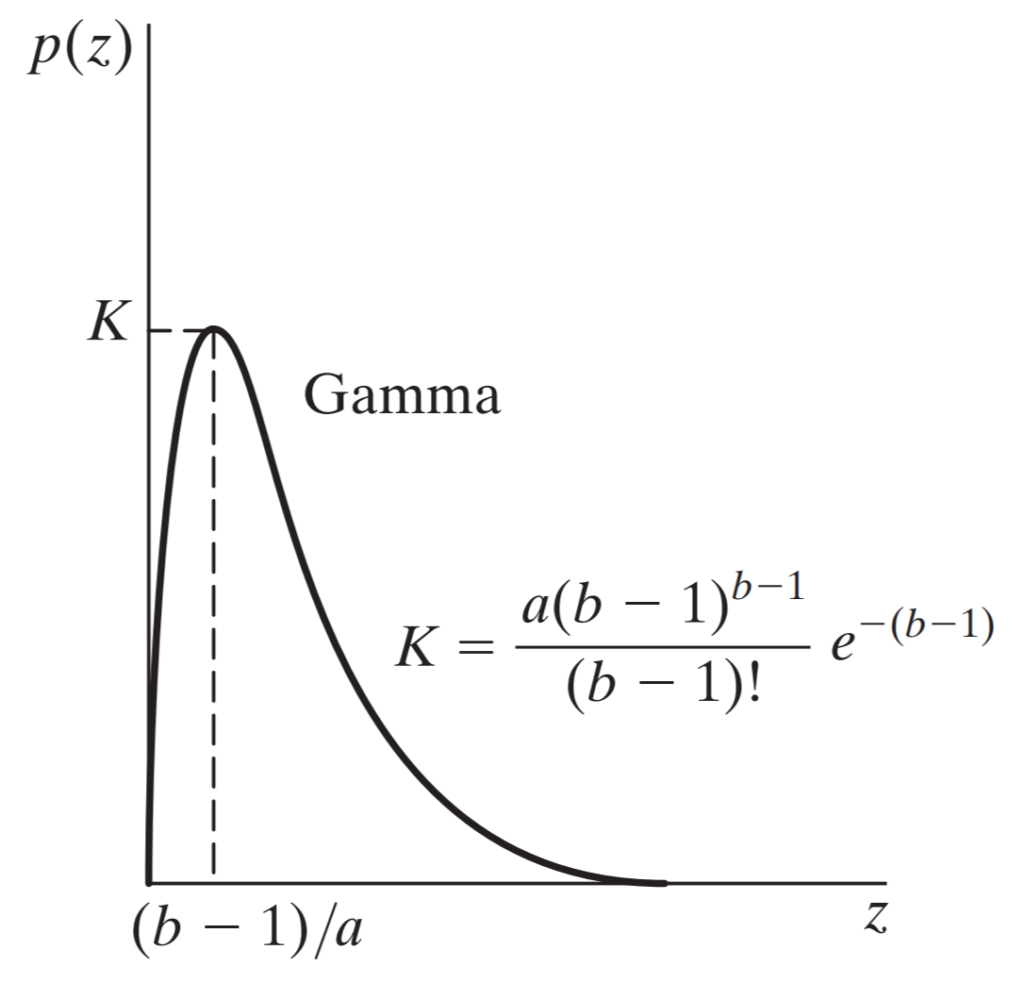
Let’s clear up a few things first before we move on to the formulation of the probability distribution function of the graph shown above.
Firstly, z axis represents the intensity values along which we distribute the noise pixel values. Secondly, a and b parameters are for shaping the curve. Now that we know what’s what, we can take a look at the function.
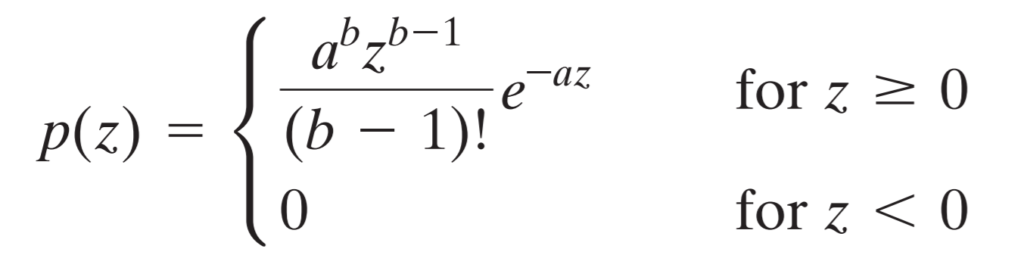
The ! below the fraction indicates the factorial of the number in the brackets and e is the Eulers constant.
I’ve written a function that makes noise with probability distribution function. I’ll break it down how it works.
Firstly, it calculates probabilities across all intensities and stores them into array. Secondly, we take those values and create an image histogram. And lastly we take all those distributed pixel values, store them into array and scramble it.
public static Bitmap GammaNoise(this Bitmap image)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
byte[] result = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
byte[] noise = new byte[bytes];
double[] erlang = new double[256];
double a = 2;
double b = 10;
Random rnd = new Random();
double sum = 0;
for (int i = 0; i < 256; i++)
{
double step = (double)i * 0.1;
if (step >= 0)
{
erlang[i] = (double)(Math.Exp(-a * step) * (Math.Pow(a, b) * Math.Pow(step, b - 1)) / NoiseDemo.Factorial((int)b - 1));
}
else
{
erlang[i] = 0;
}
sum += erlang[i];
}
for (int i = 0; i < 256; i++)
{
erlang[i] /= sum;
erlang[i] *= bytes;
erlang[i] = (int)Math.Floor(erlang[i]);
}
int count = 0;
for (int i = 0; i < 256; i++)
{
for (int j = 0; j < (int)erlang[i]; j++)
{
noise[j + count] = (byte)i;
}
count += (int)erlang[i];
}
for (int i = 0; i < bytes - count; i++)
{
noise[count + i] = 0;
}
noise = noise.OrderBy(x => rnd.Next()).ToArray();
for (int i = 0; i < bytes; i++)
{
result[i] = (byte)(buffer[i] + noise[i]);
}
Bitmap result_image = new Bitmap(w, h);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
Marshal.Copy(result, 0, result_data.Scan0, bytes);
result_image.UnlockBits(result_data);
return result_image;
}The reason we make noise artificially is to find best restoration and reconstruction techniques on all types of data. You’re able to download the project and examine the code yourself.