How To Use Laplacian Filter – C# Guide
We use Laplacian filter to sharpen images. We are going to talk about the details how exactly this filter works. In essence, it’s one of the highpass filters, which...
Filter by Category
We use Laplacian filter to sharpen images. We are going to talk about the details how exactly this filter works. In essence, it’s one of the highpass filters, which...
Gaussian highpass filter processes images in frequency domain. It attenuates low frequencies without creating ringing artifacts.
Butterworth highpass filter is used to filter images in frequency domain. We can control how smooth transition beyond cut off frequency.
Ideal highpass filter is used to filter images in the frequency domain. It attenuates low frequencies and keeps high frequencies.
We’ve talked about ideal lowpass filter and Butterworth lowpass filter already. And now, we shall get to know the last type of lowpass filters, which is Gaussian lowpass...
Butterworth lowpass filter is used to modify images in the frequency domain.
Ideal lowpass filter is a filter used to modify frequency values in the frequency domain, and for transforming an image into a frequency domain, we have to use Fourier transform....
We use Laplacian filter to sharpen images. We are going to talk about the details how exactly this filter works. In essence, it’s one of the highpass filters, which attenuate low frequencies and pass through high frequencies.
It can be applied in spatial domain as well, but we’re going to focus on applying it in the frequency domain in this tutorial.
We need to transform the image with Fourier transform, if we want to filter images in the frequency domain.
Fourier transform creates a 2 dimensional map of frequency values in a form of complex numbers. When we filter images in frequency domain we modify these values with filters. And after that, we use inverse Fourier transform to bring it back into spatial domain.
Filtering in the frequency domain works by multiplying all frequency values with the filter formula. But with Laplacian filter, this process is a little bit more complicated than that when it comes to getting our final result.
Now, let’s get into the details of applying the Laplacian filter. First of all, we need to normalize pixel values and bring their range down between 0 and 1. For which we will use the following formula.
As you can see, we need to find maximum and minimum values first before we can compute normalized values. Following function demonstrates this concept in action.
public static float[][][] Normalize_Image(this Bitmap image)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
float[][][] result = new float[3][][];
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int max = buffer.Max();
int min = buffer.Min();
int pixel_position;
for (int c = 0; c < 3; c++)
{ result[c] = new float[w][];
for (int x = 0; x < w; x++)
{
result[c][x] = new float[h];
for (int y = 0; y < h; y++)
{
pixel_position = x * 3 + y * image_data.Stride;
result[c][x][y] = ((float)buffer[pixel_position + c] - min) / (max - min);
}
}
}
return result;
}Next step is to use Fourier transform on these normalized data. But for that to work, we need to write transform functions that will take jagged array of float values instead of Bitmap images.
Following functions are modified for transforming normalized data.
public static Complex[][] Forward(float[][][] normalized_image, int channel = 0)
{
var p = new Complex[Size][];
var f = new Complex[Size][];
var t = new Complex[Size][];
var complex_image = ToComplex(normalized_image, channel);
for (int l = 0; l < Size; l++)
{
p[l] = Forward(complex_image[l]);
}
for (int l = 0; l < Size; l++)
{
t[l] = new Complex[Size];
for (int k = 0; k < Size; k++)
{
t[l][k] = p[k][l];
}
f[l] = Forward(t[l]);
}
return f;
}public static Complex[][] ToComplex(float[][][] normalized_image, int channel)
{
Complex[][] result = new Complex[Size][];
for (int x = 0; x < Size; x++)
{
result[x] = new Complex[Size];
for (int y = 0; y < Size; y++)
{
result[x][y] = new Complex(normalized_image[channel][x][y], 0);
}
}
return result;
}Next step is to multiply Laplacian filter formula with each of the frequency values. And to do that we will use the following formula that calculates values with respect to the center of the map.
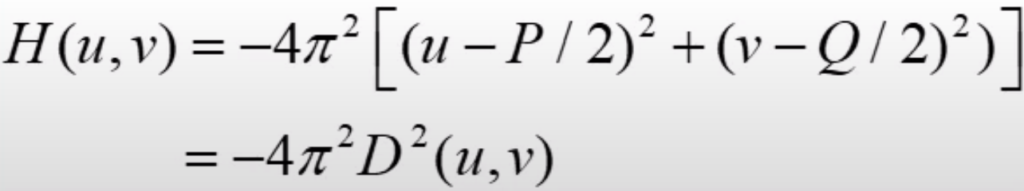
P and Q values in the formula above represent the width and height of the frequency map. They are also the same as width and height of the image we’re transforming. Following function show’s how we implement it.
public static Complex[][][] Laplacian_Filter(Complex[][][] frequencies)
{
int channels = 3;
Complex[][][] filtered = frequencies;
for (int c = 0; c < channels; c++)
{
for (int u = 0; u < Size; u++)
{
for (int v = 0; v < Size; v++)
{
double d = Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2);
filtered[c][u][v] *= (float)(-4.0 * Math.Pow(Math.PI, 2) * d);
}
}
}
return filtered;
}Now that we have filtered the data, we need to bring it back to spatial domain with inverse Fourier transform. But because we normalized the data before we transformed it, we need to modify inverse transform function as well.
public static float[][][] InverseToFloat(Complex[][][] frequencies)
{
float[][][] result = new float[3][][];
for (int i = 0; i < 3; i++)
{
var p = new Complex[Size][];
var f = new Complex[Size][];
var t = new Complex[Size][];
for (int l = 0; l < Size; l++)
{
p[l] = Inverse(frequencies[i][l]);
}
for (int l = 0; l < Size; l++)
{
t[l] = new Complex[Size];
for (int k = 0; k < Size; k++)
{
t[l][k] = p[k][l] / (Size * Size);
}
f[l] = Inverse(t[l]);
}
result[i] = new float[Size][];
for (int x = 0; x < Size; x++)
{
result[i][x] = new float[Size];
for (int y = 0; y < Size; y++)
{
result[i][x][y] = Complex.Modulus(f[x][y]);
}
}
}
return result;
}Now that we transformed the data back into the spatial domain, we need to scale it. We do that by dividing all values by max value in the array.
The next step in the process is to add together the normalized data and the filtered data. Following function shows how.
public static float[][][] Add(this float[][][] a, float[][][] b)
{
int c = -1;
float[][][] result = new float[3][][];
for (int i = 0; i < 3; i++)
{
result[i] = new float[FFT.Size][];
for (int j = 0; j < FFT.Size; j++)
{
result[i][j] = new float[FFT.Size];
for (int k = 0; k < FFT.Size; k++)
{
result[i][j][k] = a[i][j][k] + c * b[i][j][k];
}
}
}
return result;
}This is the final step in the process. Now we should have a jagged array with image data in the spatial domain. But to display it we need to scale it to range between 0 and 255, for which we will use formula for feature scaling.
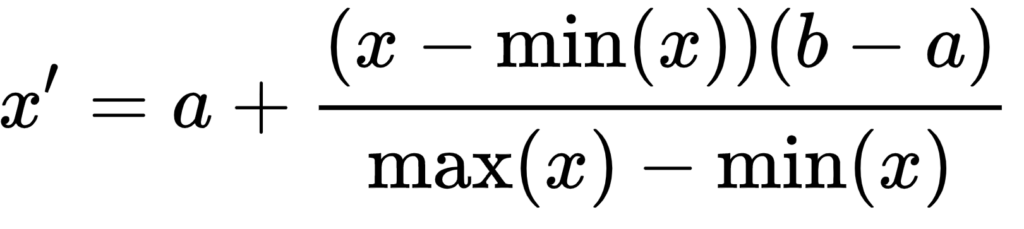
It’s very similar to normalization formula we used earlier. There are also a and b variables that represent minimum and maximum value of the desired range. And since we need to bring our data between 0 and 255 we just need to use basic normalization formula and multiply it by 255.
public static Bitmap ToImage(this float[][][] data)
{
int s = FFT.Size;
Bitmap result = new Bitmap(s, s);
BitmapData img_data = result.LockBits(
new Rectangle(0, 0, s, s),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
int bytes = img_data.Stride * img_data.Height;
byte[] buffer = new byte[bytes];
float min = 255f;
float max = 0f;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < FFT.Size; j++)
{
for (int k = 0; k < FFT.Size; k++)
{
min = Math.Min(min, data[i][j][k]);
max = Math.Max(max, data[i][j][k]);
}
}
}
for (int c = 0; c < 3; c++)
{
for (int x = 0; x < FFT.Size; x++)
{
for (int y = 0; y < FFT.Size; y++)
{
int pixel_position = x * 3 + y * img_data.Stride;
buffer[pixel_position + c] = (byte)(255 * (data[c][x][y] - min) / (max - min));
}
}
}
Marshal.Copy(buffer, 0, img_data.Scan0, bytes);
result.UnlockBits(img_data);
return result;
}Hopefully this step by step guide to filter images with Laplacian filter was helpful and instructive. You can download the entire project and examine the code yourself.