How To Use Contraharmonic Mean Filter – C# Guide
We can use contraharmonic mean filter to process image data in spatial domain. It's most effective against salt and pepper noise.
Filter by Category
We use contraharmonic mean filter to process image data in spatial domain. Therefore we will need to use kernel and convolution to apply it. We could also say that it’s the most useful for removing impulse or salt and pepper noise.
Mean filters are in general most useful to deal with images that only have noise degradation. In other words, image alterations of any other kind might complicate restoration process.
Kernel and convolution are essential for filtering in spatial domain. I’ll try to keep it short and simple about it, but I also recommend you get to know how it works in detail.
Kernel is basically a small matrix we put on top of our image. It works as a window to take values in a local area of the image and compute one output value from each position. This is also the reason why spatial filtering outputs images with slightly smaller dimensions.
Convolution is the process of calculating the values from kernel and image to compute new output value. We also move kernel along the entire image to compute all output values to form the image.
As we mentioned before, contraharmonic mean filter is most effective to use for images with salt and pepper noise. While harmonic mean filter deals with salt noise and fails for the pepper noise, this one works for both.
However, we can’t use it to remove both at the same time. Let’s take a look at the following formula to understand better how it works.
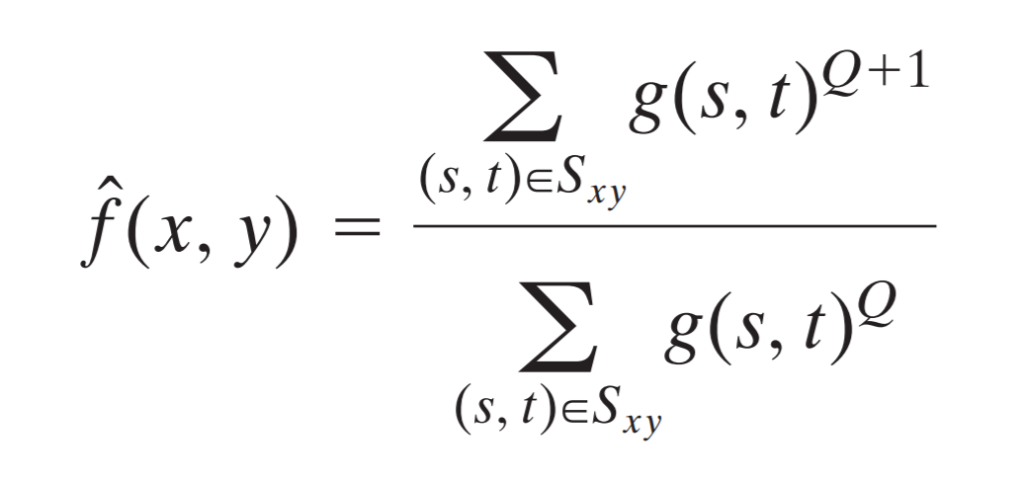
The g(s, t) function represents pixel value from corrupted image, while s and t variables represent the coordinates inside the kernel.
There is also Q variable in this formula, which is something extra and only this mean filter has it. Furthermore, it represents the order of the filter. If we set it to positive number, it’s going to remove pepper noise and if we set it to negative, it’s going to remove salt noise.
If we set Q to 0, it’s going to reduce the filter into arithmetic mean filter and if we turn it to -1, it’s going to become harmonic mean filter.
Therefore, to remove salt and pepper noise, we need to use this filter twice to remove each individually.
public static Bitmap ContraharmonicMean(this Bitmap image, double order)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int r = 1;
int wres = w - 2 * r;
int hres = h - 2 * r;
Bitmap result_image = new Bitmap(wres, hres);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, wres, hres),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
int res_bytes = result_data.Stride * result_data.Height;
byte[] result = new byte[res_bytes];
for (int x = r; x < w - r; x++)
{
for (int y = r; y < h - r; y++)
{
int pixel_location = x * 3 + y * image_data.Stride;
int res_pixel_loc = (x - r) * 3 + (y - r) * result_data.Stride;
double[] sum1 = new double[3];
double[] sum2 = new double[3];
for (int kx = -r; kx <= r; kx++)
{
for (int ky = -r; ky <= r; ky++)
{
int kernel_pixel = pixel_location + kx * 3 + ky * image_data.Stride;
for (int c = 0; c < 3; c++)
{
sum1[c] += Math.Pow(buffer[kernel_pixel + c], order + 1);
sum2[c] += Math.Pow(buffer[kernel_pixel + c], order);
}
}
}
for (int c = 0; c < 3; c++)
{
result[res_pixel_loc + c] = (byte)(sum1[c] / sum2[c]);
}
}
}
Marshal.Copy(result, 0, result_data.Scan0, res_bytes);
result_image.UnlockBits(result_data);
return result_image;
}Contraharmonic mean filter is one of the filters we can use to turn into others if we need it. Therefore, it’s a kind of universal filter for processing salt and pepper noise. However, it has some shortcomings, such as we need to know if the noise is light or dark to set the order of it right.
I hope this guide was helpful. You can also download the entire project and try it out on your own images.