How To Make Gaussian Noise On Image – C# Guide
Gaussian noise on images is generated with Gaussian probability distribution function. It simulates noise that appears in practice.
Filter by Category
Gaussian noise is a great approximation to noise we get from taking a photo. In other words, our sensoring equipment is sometimes affected by a veriety of factors. These are usually the quality of equipment and environmental conditions.
For instance, a charged coupled device – camera is sensitive to light levels and temperature changes. These affect the quality of photos the most. But they aren’t the only reason why we could get a corrupted image.
Our images can also get corrupted in the transmission. Most commonly when we’re transmitting wirelessly, where lightning and other atmospheric disturbances can physically influence our signal.
When we gather a large amount of data about a certain event or events in nature, we can often see the pattern of Gaussian distribution. We also call it normal distribution and we’re going to use it to calculate random values for our Gaussian noise.
The following formula is our Gaussian probability distribution function.
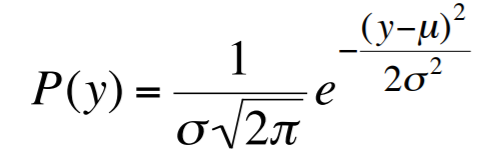
If we look at the formula there are 3 unknown varibales, which are σ (sigma), y and μ (mi). Sigma and mi represent standard deviation and mean which affect the position and width of distributed values.
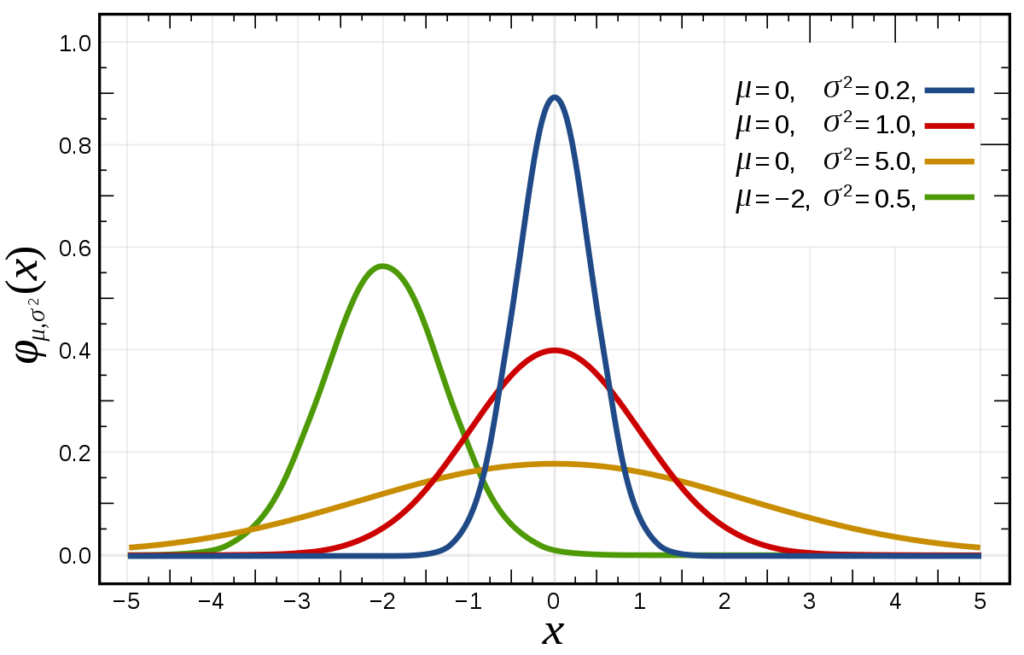
As you can see from the formula that we use standard deviation to the power of 2, which is variance of the distribution. The only unknown we haven’t explained yet is y, which is our random variable. Therefore, we need to generate this number with random number generator class.
I feel we should also mention, that the sum of all calculated values in the distribution curve equals to 1. Therefore, we will also need to bring those values to displayable range for our image noise.
We can do that with formula for feature scaling which we already used before in tutorial for Laplacian filter in frequency domain.
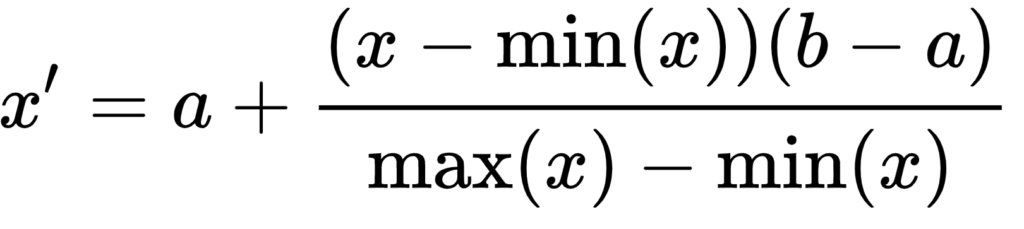
Once we generate Gaussian noise, we need to apply it to our image. We can do that by summing the image pixel values with generated noise value.

I wrote an extension function that takes our original image as input and adds noise to it and outputs the final result.
public static Bitmap GaussianNoise(this Bitmap image)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
byte[] result = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
byte[] noise = new byte[bytes];
double[] gaussian = new double[256];
int std = 20;
Random rnd = new Random();
double sum = 0;
for (int i = 0; i < 256; i++)
{
gaussian[i] = (double)((1 / (Math.Sqrt(2 * Math.PI) * std)) * Math.Exp(-Math.Pow(i, 2) / (2 * Math.Pow(std, 2))));
sum += gaussian[i];
}
for (int i = 0; i < 256; i++)
{
gaussian[i] /= sum;
gaussian[i] *= bytes;
gaussian[i] = (int)Math.Floor(gaussian[i]);
}
int count = 0;
for (int i = 0; i < 256; i++)
{
for (int j = 0; j < (int)gaussian[i]; j++)
{
noise[j + count] = (byte)i;
}
count += (int)gaussian[i];
}
for (int i = 0; i < bytes - count; i++)
{
noise[count + i] = 0;
}
noise = noise.OrderBy(x => rnd.Next()).ToArray();
for (int i = 0; i < bytes; i++)
{
result[i] = (byte)(buffer[i] + noise[i]);
}
Bitmap result_image = new Bitmap(w, h);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
Marshal.Copy(result, 0, result_data.Scan0, bytes);
result_image.UnlockBits(result_data);
return result_image;
}Gaussian noise is one of the most tractable noise distribution models we use in practice. In other words, it’s very useful for simulating real life data of certain events like random noise on images, or other signals.
You can also download the project for free and examine the code yourself.