How To Use Butterworth Highpass Filter – C# Guide
Butterworth highpass filter is used to filter images in frequency domain. We can control how smooth transition beyond cut off frequency.
Filter by Category
Butterworth highpass filter is used to filter images in frequency domain. We can control how smooth transition beyond cut off frequency.
Ideal highpass filter is used to filter images in the frequency domain. It attenuates low frequencies and keeps high frequencies.
We’ve talked about ideal lowpass filter and Butterworth lowpass filter already. And now, we shall get to know the last type of lowpass filters, which is Gaussian lowpass...
Butterworth lowpass filter is used to modify images in the frequency domain.
Ideal lowpass filter is a filter used to modify frequency values in the frequency domain, and for transforming an image into a frequency domain, we have to use Fourier transform....
Fourier transform is an equation that turns normal pixel values into complex numbers. But to know what these complex numbers mean, we should give a little more context to them by...
C# tutorial on how to achieve histogram equalization on an image.
In this tutorial we will be talking about intensity level slicing in image processing. What is Intensity Level Slicing It’s a process that highlights pixels in an arbitrary...
This post is a short revision of Contrast Stretch post we already worked on in the past. Where we talked about histogram equalization, which is a little more complex method than...
What is Log Transformation Anyway? Log transformation in image processing is a part of gray level transformations. It works by transforming each pixel individually. It is usually...
Butterworth highpass filter is just one of the highpass filters. We use these type of filters for filtering data in the frequency domain.
I’ve talked about transforming the images into frequency domain more in detail on a post about Fourier transform. If we convert image data into frequency domain we get a map of complex numbers. And when we talk about filtering data in the frequecy domain, it simply means we multiply each complex number in the map with a filter formula.
If you take a look at ideal highpass filter, it basically cuts out a hole in the middle of a Fourier transform. Butterworth has a similar effect on the transform. It differs at the transition between frequencies we want to cut out and those we don’t.

What makes Butterworth highpass filter special is that smooth transition between high and low frequencies. It does require an additional parameter we need to set, which is the order of the filter.
Let’s take a look what the filter formula looks like and dissect it, so we’ll get a better understanding how it works.
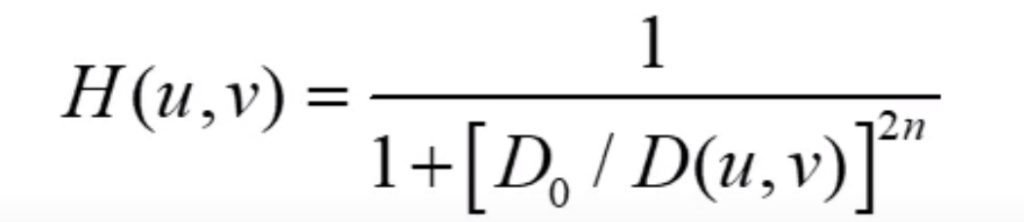
Okay, so the formula above might look a little daunting, but don’t worry we’ll go through it piece by piece.
First of all, the u and v variables represent the coordinates on a frequency map that we get from Fourier transformation. Going forward, let’s take a look what’s going on below the fraction.
The n is the order we mentioned earlier. So the larger the order is, the more filter acts as an ideal highpass filter. It’s the controllable part that sets the width of the fade between the frequencies we want cut out and those we don’t.
D0 represents our cut off frequency and it stands for distance from center or in other words, the radius of the circle in the middle.
The D(u, v) is the distance from the center of each frequency on the map given the position of the coordinates. We can calculate it by the following formula.
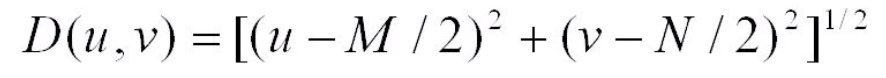
The M and N expressions represent the width and height of the frequency map, which in our case are the same since our fast fourier transform algorithm only accepts square images.
The following function takes a 3 dimensional jagged array of complex numbers. Therefore we need to make 3 frequency maps, one for each color channel.
public static Complex[][][] Butterworth_Highpass_Filter(Complex[][][] frequencies, double distance, int order)
{
int channels = 3;
Complex[][][] filtered = frequencies;
for (int c = 0; c < channels; c++)
{
for (int u = 0; u < Size; u++)
{
for (int v = 0; v < Size; v++)
{
double d = Math.Sqrt(Math.Pow(u - Size / 2, 2) + Math.Pow(v - Size / 2, 2));
filtered[c][u][v] *= (float)(1 / (1 + Math.Pow(distance / d, 2 * order)));
}
}
}
return filtered;
}If we compare it to the function for Butterworth lowpass filter, we can see it’s almost identical. The only difference is that the cut off frequency and calculated distance from center at any given position are swapped.
You can download the entire project and play with the values. The project also includes all code for fast Fourier transform, without which all this wouldn’t work anyway.