How To Use Harmonic Mean Filter On Images – C# Guide
Harmonic mean filter is of mean filters we can use to process image data in spatial domain. This guide shows how to apply it with C#.
Filter by Category
Harmonic mean filter is of mean filters we can use to process image data in spatial domain. This guide shows how to apply it with C#.
Geometric mean filter is one of mean filters we can use processing images in spatial domain. We use C# programming language to apply it here.
Arithmetic mean filter is one of the simplest mean filters we could use to reduce noise from an image. Learn more about spatial filtering.
Salt and pepper noise or impulse noise is one of the noise models we can use to simulate image data corruption in real life.
Uniform noise is one of the noise models we can use to simulate real life data corruption. This guide shows how to make in on images.
Exponential noise is one of the noise models we can use to simulate corruption of data. This guide show how to use it on images.
Gamma noise is one of the noise models we use to simulate practical data corruption. This guide shows how to apply it on images.
Rayleigh noise is one of the noise models with which we can simulate data corruption. Guide to making noise from PDF and image histogram.
Gaussian noise on images is generated with Gaussian probability distribution function. It simulates noise that appears in practice.
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired...
Harmonic mean filter is one of the mean filters we use to process image data in spatial domain. Therefore, like with most of spatial filters, we will need to use a kernel and convolution.
With mean filters in general, we essentially blur the image to deal with noise corruption. Therefore, we should use them for images that have only this kind of degradation. In other words, having any other alterations in the image might complicate the process of restoring it to its original form.
We mentioned, we will need kernel and convolution. In case you’re not familiar with any of it, I’ll try and keep it short and concise, but I recommend you learn more in detail if anything remains unclear.
Kernel is a small matrix, we put on top of our image pixel values. It’s like a window, with which we take those values inside it to compute a new output pixel value. Calculating values together on each kernel position only produces one output pixel value.
Furthermore, to produce the entire output image, we need to use convolution. It’s essentially the process of moving the kernel one pixel at a time and calculating new output pixel values.
However, there is a downside to this process, because the output image will have a little smaller dimensions. But we can’t use zero padding with this filter because it would require to divide by 0, and it’s just not worth ending the world like this.
We can use harmonic mean filter to remove salt noise. Similar to salt and pepper noise also known as impulse noise, without probability of impulses of lower intensities. However, it fails for the pepper noise.
Let’s take a look at the following formula that computes new pixel values.
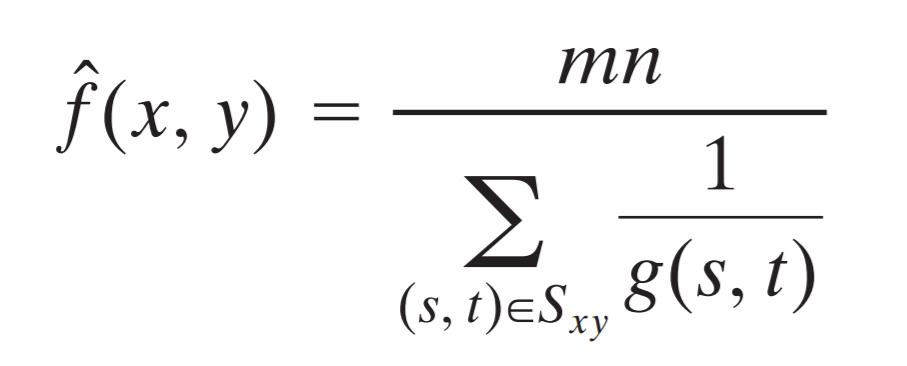
The g(s, t) represents each pixel value inside the kernel, s and t being relative coordinates of the kernel itself.
public static Bitmap HarmonicMean(this Bitmap image)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int r = 1;
int wres = w - 2 * r;
int hres = h - 2 * r;
Bitmap result_image = new Bitmap(wres, hres);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, wres, hres),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
int res_bytes = result_data.Stride * result_data.Height;
byte[] result = new byte[res_bytes];
for (int x = r; x < w - r; x++)
{
for (int y = r; y < h - r; y++)
{
int pixel_location = x * 3 + y * image_data.Stride;
int res_pixel_loc = (x - r) * 3 + (y - r) * result_data.Stride;
double[] mean = new double[3];
for (int kx = -r; kx <= r; kx++)
{
for (int ky = -r; ky <= r; ky++)
{
int kernel_pixel = pixel_location + kx * 3 + ky * image_data.Stride;
for (int c = 0; c < 3; c++)
{
mean[c] += 1d / buffer[kernel_pixel + c];
}
}
}
for (int c = 0; c < 3; c++)
{
result[res_pixel_loc + c] = (byte)(Math.Pow(2 * r + 1, 2) / mean[c]);
}
}
}
Marshal.Copy(result, 0, result_data.Scan0, res_bytes);
result_image.UnlockBits(result_data);
return result_image;
}Harmonic mean filter is useful for removing impulses on a higher end of intensity range. I hope this guide was helpful and I hope you’ll read some of my other posts as well.
You can download the project and try it out on your own images.