How To Use Geometric Mean Filter On Image – C# Guide
Geometric mean filter is one of mean filters we can use processing images in spatial domain. We use C# programming language to apply it here.
Filter by Category
Geometric mean filter is one of mean filters we can use processing images in spatial domain. We use C# programming language to apply it here.
Arithmetic mean filter is one of the simplest mean filters we could use to reduce noise from an image. Learn more about spatial filtering.
Salt and pepper noise or impulse noise is one of the noise models we can use to simulate image data corruption in real life.
Uniform noise is one of the noise models we can use to simulate real life data corruption. This guide shows how to make in on images.
Exponential noise is one of the noise models we can use to simulate corruption of data. This guide show how to use it on images.
Gamma noise is one of the noise models we use to simulate practical data corruption. This guide shows how to apply it on images.
Rayleigh noise is one of the noise models with which we can simulate data corruption. Guide to making noise from PDF and image histogram.
Gaussian noise on images is generated with Gaussian probability distribution function. It simulates noise that appears in practice.
We can use notch filters for attenuating frequencies on custom locations across the frequency map. But for that we will need to utilize all of the knowledge we’ve acquired...
Bandpass filters are the counterpart of bandreject filters. Therefore, they attenuate every frequency outside the ring. In case you’re just tuning in, let me clarify what I...
We’re going to use geometric mean filter to process image data in the spatial domain. In general, the effect it has on image is pretty similar to that of arithmetic mean filter.
Mean filters are most useful for processing images which only have noise corruption. Their effect in general is to smooth or blur our image. This is also where geometric mean filter differs arithmetic one. While smoothing, it doesn’t lose as much image detail data.
Filtering data in the spatial domain means we will need to use convolution and a kernel. Firstly, convolution is the process in which we’re going to move our kernel along the entire image. And secondly, kernel is a small window we place on top of our image pixel values.
We usually use filter specific coefficients to multiply with pixel values and sum them together. But in our case, we will multiply all values inside the kernel together. And after that we will raise it to the power of 1/mn, m and n being the dimensions of our kernel.
Let’s take a look at the formula that does all the work.
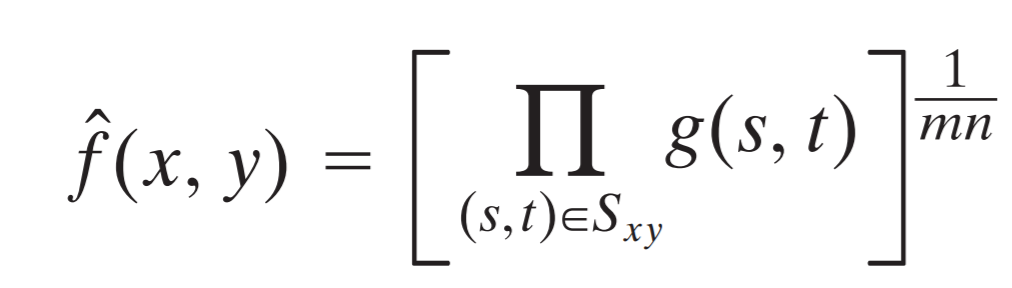
Formula above presents us how to calculate a new pixel value, which we will place in the center of our kernel. The process inside the brackets is what we described above. Therefore, g(s, t) represents the location of each pixel value inside the kernel located at coordinates s and t.
We should also mention that our image will reduce in size after processing it, unless we would use zero padding to compensate for those lost pixels.
I’ve written a function that applies the geometric mean filter. However, I had to make some modifications to the zero padding function. I changed so it pads the image with pixels that have value of 1. Therefore, if we’re technically correct, it becomes function for one padding rather than zero padding.
public static Bitmap GeometricMean(this Bitmap image)
{
int w = image.Width;
int h = image.Height;
BitmapData image_data = image.LockBits(
new Rectangle(0, 0, w, h),
ImageLockMode.ReadOnly,
PixelFormat.Format24bppRgb);
int bytes = image_data.Stride * image_data.Height;
byte[] buffer = new byte[bytes];
Marshal.Copy(image_data.Scan0, buffer, 0, bytes);
image.UnlockBits(image_data);
int r = 1;
int wres = w - 2 * r;
int hres = h - 2 * r;
Bitmap result_image = new Bitmap(wres, hres);
BitmapData result_data = result_image.LockBits(
new Rectangle(0, 0, wres, hres),
ImageLockMode.WriteOnly,
PixelFormat.Format24bppRgb);
int res_bytes = result_data.Stride * result_data.Height;
byte[] result = new byte[res_bytes];
for (int x = r; x < w - r; x++)
{
for (int y = r; y < h - r; y++)
{
int pixel_location = x * 3 + y * image_data.Stride;
int res_pixel_loc = (x - r) * 3 + (y - r) * result_data.Stride;
double[] mean = new double[3];
for (int i = 0; i < mean.Length; i++)
{
mean[i] = 1;
}
for (int kx = -r; kx <= r; kx++)
{
for (int ky = -r; ky <= r; ky++)
{
int kernel_pixel = pixel_location + kx * 3 + ky * image_data.Stride;
for (int c = 0; c < 3; c++)
{
mean[c] *= buffer[kernel_pixel + c];
}
}
}
for (int c = 0; c < 3; c++)
{
result[res_pixel_loc + c] = (byte)Math.Pow(mean[c], 1 / Math.Pow(2 * r + 1, 2));
}
}
}
Marshal.Copy(result, 0, result_data.Scan0, res_bytes);
result_image.UnlockBits(result_data);
return result_image;
}Geometric mean filter is just one of many mean filters we use for filtering image data in spatial domain. It blurs the image slightly, having a similar effect than arithmetic mean filter, but without losing as much details.
You can also download the project and try it out on your images. I hope this tutorial was helpful and understanding.